Faz Farkı

Fourier Serisi üzerine

Hayatımızın herhangi bir alanında bir bütünü alt parçalarıyla görmek, analiz etmek gerekebiliyor. Elektronik ve haberleşmede kullanılan işaretler için en temel analiz frekans içeriğinin belirlenmesidir. Farklı farklı frekans cevabına sahip devre/sistemlerin işaret üzerinde nasıl bir etki yapacağı işaretin frekans içeriğinin bilinmesiyle anlaşılabilmektedir. Örneğin aşağıdaki resimde üst resimdeki sinyal bir kablodan geçtikten sonra alt resimdeki gibi olmaktadır. Kablonun frekans cevabı ve işaretin frekans içeriği bilindiğinde çıkış işaretinin alt resimdeki işaret gibi olacağı bulunabilmektedir.

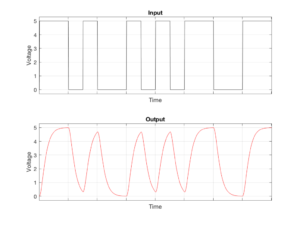
Sinyal sistemlerle uğraşıyor olmamız şart değildir, günlük hayatımızda maruz kaldığımız işaretlerin frekans içeriği çoğu zaman farkında olmasak bile bizi ilgilendirmektedir. Mesela, kulağımıza gelen ses dalgalarının (mekanik titreşimler) frekans içeriği bizi ilgilendirir; şöyle ki ses içerisinde olabilecek yüksek frekanslı bileşenlerden (tiz sesler) rahatsız oluruz.
Kulağımız belirli frekans aralığındaki sesleri duyabilmektedir. Gözümüze gelen elektromagnetik dalgalardan sadece belirli frekans aralığında olanları görebiliriz… Çevremizde şu anda işitme aralığımızın dışında birçok ses olabileceği gibi görme aralığımızın dışında birçok elektomagnetik dalga vardır. Bir ultrasonik vericinin yaydığı ses dalgaları, havadaki radyo dalgaları veya bir IR ledden yayılan dalgalar hemen verebileceğimiz algılama aralığımız dışına çıkan örneklerdendir. Bir başka örnek, güneşimizden dünyamıza çok geniş spektrumda yayın gelmektedir ancak biz sadece görme aralığımızdaki yayınları görebilmekteyiz. 
Peki işitme aralığımızı sınırlayan nedir? Kulak zarımızın bu sınırlar dışında titreşmiyor olması mıdır? Belki de kulak zarımız titreşiyor ancak beynimiz o frekansları algılayamıyordur? Cevabı bilmiyorum ancak işin içine sistemdeki bileşenlerin frekans cevapları girdi bile. Kendimizden örnekler verdiğimiz gibi kullandığımız her devre veya sistemin bir frekans cevabı vardır.

Bu yazıda öncelikle periyodik işaretler üzerinden gideceğiz.
Periyodik işaretlerin frekans içeriği ayrık frekans bileşenlerinden oluşur, örneğin 3 KHz’lik periyodik bir işaret içerisinde 3 KHz, 6 KHz, 9 KHz…ve katları frekans bileşenleri bulunmaktadır. Bu bileşenler Fourier serisini oluşturmaktadır.
Periyodik olmayan işaretlerde frekans içeriği frekansın sürekli bir fonksiyonu olur, bu durumda Fourier serisinden değil Fourier dönüşümden bahsedilir. Fourier serileri üzerinde çalışıldıktan sonra periyodik bir işaretin periyodunu sonsuza götürüp periyodik olmayan bir işarete benzettikçe ayrık olan frekans bileşenlerinin birbirine yaklaşmaya ve ayrık spektrumdan sürekli spektruma yaklaştığını gözlemek mümkün olacaktır. Kısacası Fourier seri çözümlemesi anlaşıldığında Fourier dönüşümünün seri çözümlemenin genelleştirilmiş hali olduğu görülebilmektedir

Fourier seri çözümlemesi bir işaretin frekans bileşenlerinin ortaya çıkarılması işlemidir. Karmaşık gibi görünse de yapılan işlem 3 boyuttaki bir vektörün x, y ve z yönlerindeki bileşenlerinin bulunmasına çok benzemektedir.

Fourier serisinin en önemli özelliği “expansion” fonksiyonlarının birbirine dik olmasıdır, seride toplanan fonksiyonlara “expansion”  fonksiyonları veya baz fonksiyonları denir. Fourier serisinin baz fonksiyonları exp(i*m*x) veya “sin(mx) ve cos(nx)” fonksiyonlarıdır (m, n tam sayı). Orthogonality (diklik) kavramını vektörlerden bilmekteyiz. Örneğin ex vektörü ile ey vektörü birbirine diktir. Genel olarak A ve B vektörü için iç çarpım sonucu A.B=0 olması bu vektörlerin dik olduğunu gösterir. Vektör boyutu 3 ü geçtiğinde diklik gözde canlandırılamaz olur ancak biliriz ki dik vektörlerin birbirine izdüşümü 0 dır, dik vektörlerin span ettiği bir uzaydaki herhangi bir vektörün bu dik vektörler üzerine izdüşümleri iç çarpım kullanılarak bulunabilir.
Vektör uzayı, baz vektörler, bir vektörün baz vektörler üzerine izdüşümleri, iç çarpım kavramları daha aşina olduğumuz kavramlar.
Fourier seri çözümlemesi ise fonksiyon uzayı, baz fonksiyonlar, bir fonksiyonun baz fonksiyonlar üzerine izdüşümü, fonksiyonların iç çarpımı kavramlarını düşünmemizi gerektirmektedir.
Fonksiyonlar, sonsuz boyutlu vektörler olarak düşünülebilir.
Vektör iç çarpımında iki vektörü karşı düşen değer değer çarpıp topluyoruz, fonksiyonumuz sonsuz boyutlu bir vektör olduğundan fonksiyonlarda iç çarpım değer değer çarpıp toplamak yerine fonksiyonları çarpıp integral almaya denk düşmektedir.

Bir f(x) ve g(x) fonksiyonunun iç çarpımı

Int f(x)*g(x)*dx integraliyle tanımlanmaktadır.

Bu fonksiyonların dik olması ise iç çarpımın 0 olma şartıyla tanımlanmaktadır:

Int f(x)*g(x)*dx =0 (f(x) ve g(x) fonkisyonları birbirine dik)

Fonksiyonların birbirine dikliği tanımlanabildiği gibi tıpkı vektörlerde olduğu gibi bir fonksiyonun başka fonksiyonlar üzerine izdüşümü de vardır. ex, ey ve ez baz vektörlerinin “span” ettiği dik koordinat sisteminde bir vektörün bu baz vektörleri üzerine ayrı ayrı izdüşümleri bulunabildiği gibi baz fonksiyonlarının oluşturduğu (span ettiği) bir uzayın fonksiyonunun bu baz fonksiyonlar üzerine izdüşümü bulunabilir. Fourier seri çözümlemesi fonksiyonumuzun (işaretimizin) baz fonksiyonları üzerine izdüşümünün bulunması işlemidir.

Örnek:

Bir A=3*ex+4*ey+5*ez vektörünü ex, ey ve ez baz vektörleri üzerine iş düşümleri(her ne kadar ifadede görülse de) A vektörünün ilgili baz vektörleri ile iç çarpımıyla bulunmaktadır:   

A*ex=3
A*ey=4 ve
A*ez=5 olarak bulunabileceği gibi bir

f(t)= 3*sin(t) + 5*sin(4t) + 10*sin(9t) fonksiyonunun sin(t), sin(2*t), sin(3*t)…baz fonksiyonları üzerine izdüşümleri(her ne kadar ifadede görülse de) f fonksiyonunun ilgili baz fonksiyonları ile iç çarpımıyla bulunmaktadır:

(2/T)*Int(f(t)*sin(t)dt)=3
(2/T)*Int(f(t)*sin(4t)dt)=5 ve
(2/T)*Int(f(9t)*sin(t)dt)=9 şeklinde bulunabilir.

Bu girişten sonra Fourier seri çözümlemesinde en önemli kavram olan baz fonksiyonlarının dikliği konusuna bakalım. Devamını getirmek ümidiyle…

Faydalı kaynaklar:

https://www.falstad.com/fourier/Fourier.html
https://www.cs.utexas.edu/users/fussell/courses/cs384g…/lecture05-Orthogonal.pdf