Faz Farkı

Filtreler

Son güncellenme: 8 Ekim 2011

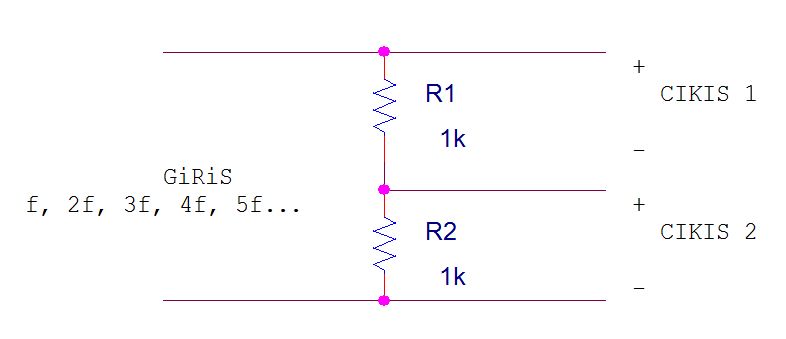
Aşağıdaki devrede girişten 10V tepe değerli sinüs uygulayalım, frekansımız f olsun, R1 ve R2 dirençleri üzerine düşen gerilimlerin(çıkış1, çıkış2) tepe değerleri 5V a 5V olur.

Frekansımızı 2f yapalım 5V a 5V kalmaya devam eder, 3f, 4f, 5f… 5V a 5V kalır çünkü frekansın değişmesi dirençlerin devredeki rolünü hiç değiştirmez, f frekansında tepkinlikleri 1k idi 10f frekansında da 1k, gerilimi aynı şekilde paylaşırlar. Ancak bunlardan bir tanesi kapasite veya bobin olsaydı durum farklı olacaktı. Bu elemanlar farklı frekanslarda farklı tepkinlik gösterir. Mesela bobin elemanının tepkinliği(empedansı) Zl=i*(2*pi*f)*L dir, yani yüksek frekanslarda yüksek tepkinlik gösterir. Tepkinliğin artması artık açık devre gibi oluyor demek, tepkinliğin azalması da artık kısa devre gibi oluyor demek.

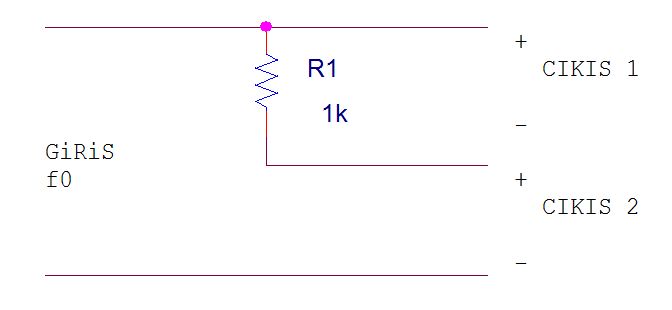
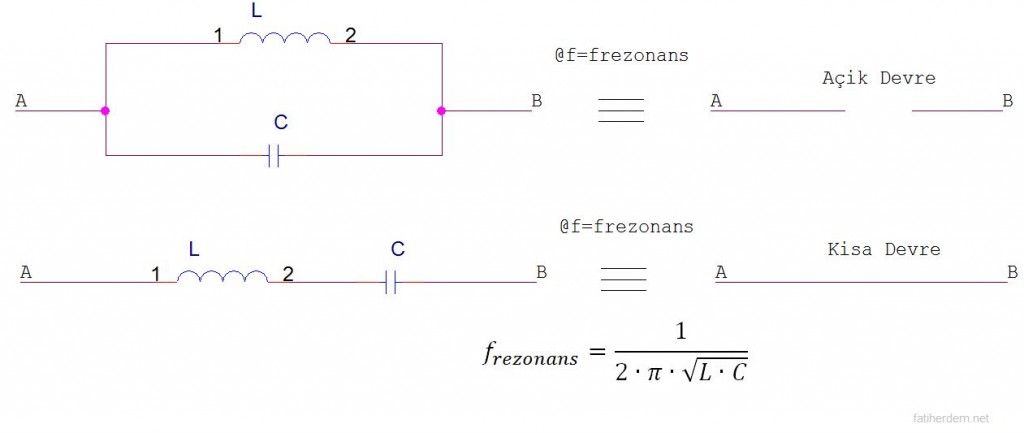
Mesela R2 nin yerine öyle bir devre koysak ki f0 frekansında tepkinliği çoook yüksek oluyor olsun, bu durumda o devreyi açık devre gibi kabul ettiğimizde devrenin f0 daki eşdeğeri aşağıdaki gibi olur:

Şu durumda f0 frekanslı(ve civarı frekanslar) giriş olduğu gibi ÇIKIŞ2 den okunur, yani giriş aynen çıkış2 ye geçer çıkış1 e hiçbir şey kalmaz. Öyle olmaz mı? R1 den akım akmıyor, giriş aynen çıkış2 den okunur.

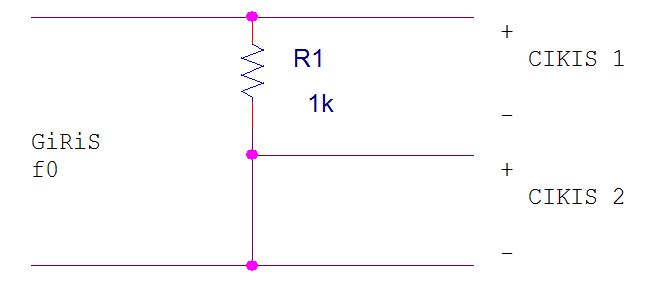
R2 yerine f0 frekansında çok düşük tepkinlik(kısa devre gibi) gösteren bir devre koymuş olsaydık, bu durumda ne olduğunu görmek için R2 yerine kısa devre koyarız:

Bu durumda ise giriş, çıkış2 de kendini hiç gösteremez, çünkü kısa devre, tüm giriş çıkış1 de belirir.

Yukarıda  f0 frekansını(ve civarını) çıkışına veren veya f0 frekansını(ve civarını) çıkışına vermeyen iki tip devreden bahsettik. Bunlar sırasıyla bant geçiren ve bant durduran filtrelerdir. (2. bahsettiğimiz bant durduranın özel bir hali olan notch filter gibi de düşünülebilir).

Peki R2 yerine koyduğumuz f0 frekansında çok yüksek tepkinlik gösteren veya çok düşük tepkinlik gösteren devreler nelerdir? Çok yüksek veya çok düşük tepkinlikleri paralel ve seri rezonans yapılarıyla elde edebiliyoruz. Mesela paralel LC devresi bir f0 frekansında çok yüksek tepkinlik gösterirken, seri LC devresi bir f0 frekansında çok düşük tepkinlik gösterir. Bu frekanslara bu devrelerin rezonans frekansı denir ve değeri f=1/(2*pi*kok(L*C)) dir. Bu ifadeyi bulmak kolaydır, paralel LC için fazörler yazısında bahsedilmişti, seri LC de ise hesaplamak daha kolay. L nin empedansı i*w*L ve C nin empedansı -i*1/(w*C), seri bağlı olduklarından eşdeğer empedans i*(w*L-1/(w*C)) olur, w*L-1/(w*C) değeri w = 1/kok(L*C) olduğunda sıfır olur(gerçekte çok çok küçük değerlere ulaşılır). w açısal frekansımız 2*pi*f tir. Paralel ve seri rezonans yapıları filtrelerde çok kullanılır.

Paralel LC ve Seri LC Rezonans Yapıları

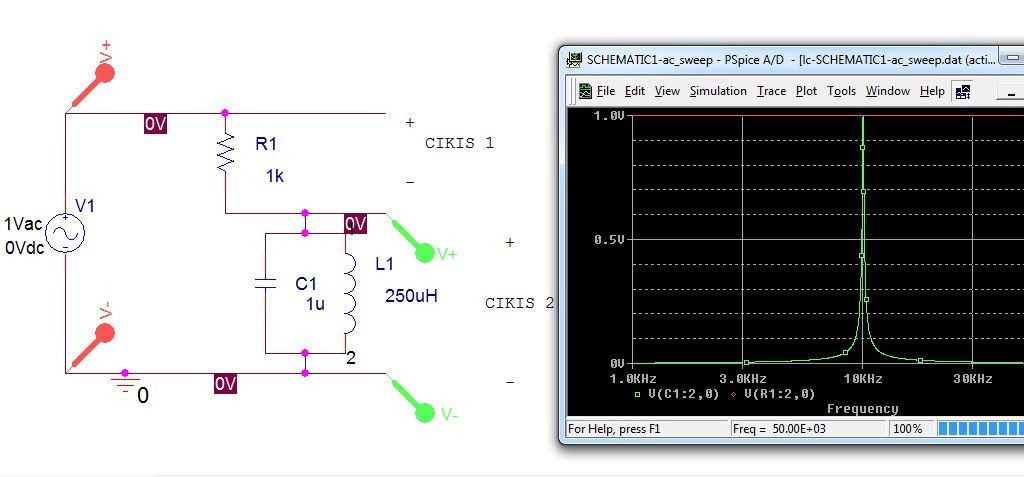
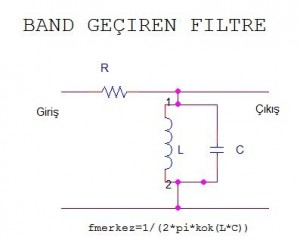
Gelin R2 yerine rezonans frekansı 10kHz olan paralel LC koyalım ve spice da AC sweep analiz yapalım: 1/(2*pi*kok(L*C)) yi 10kHz yapacak L ve C değerini 250 uH ve 1uF olarak seçelim:

1V luk bir kaynağın frekansını 1kHz ve 30kHz arasında değiştirerek taradık ve en yüksek çıkışın 10kHz de olduğunu gördük, 10kHz de rezonans yapımız açık devre gibi davrandığından o frekansta girişteki 1V tepe değerlikli sinüs çıkışta kendisini aynen gösteriyor. 10KHz merkez frekanslı bir bantgeçiren filtremiz oldu. 1k lık R1 direncinin değeri bu cevabı çok etkiler, nasıl etkilediği üzerine düşünebiliriz.

Paralel LC yerine değerleri değiştirmeden seri LC yapsaydık, rezonans frekansı aynı ancak artık rezonans frekansında çok düşük tepkinlik gösteren bir devremiz olacaktı, bu yapıda 10kHz de çıkışı neredeyse 0 da görecektik. R1 direnci o devrede  de etkili rol oynuyor, direnci düşürdükçe filtre cevabı keskinleşecektir.

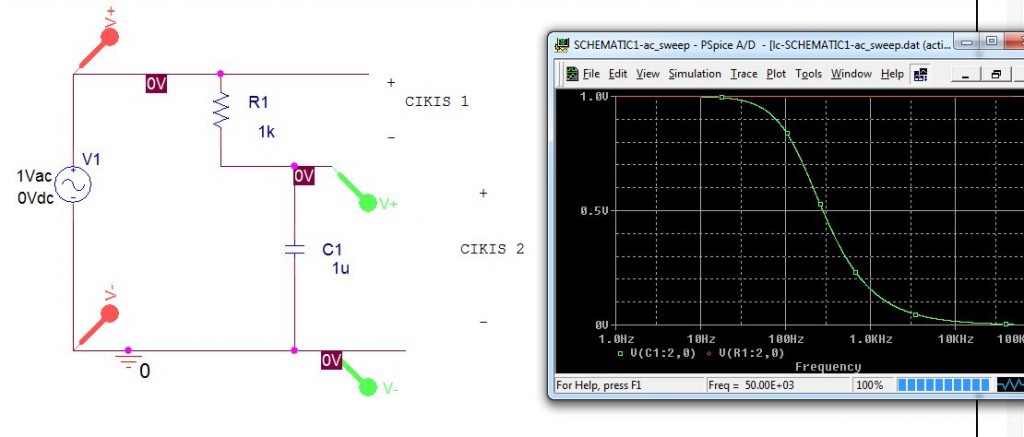
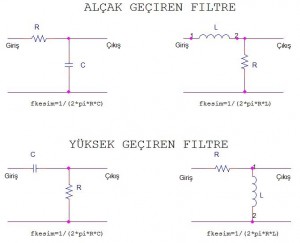
Basit alçak geçiren yüksek geçiren devrelerimizde rezonans yapıları yerine tepkinliği frekansa göre artan/azalan elemanlar koyarak filtreleme yapıyoruz, mesela aşağıdaki yapıya bakalım, R2 yerine bir C elemanı koymuş olsaydık:

Verdiğimiz ilk örnekte R1, R2 gerilim bölücü devrede f, 2f, 3f frekanslarında gerilim eşit bölünürken burda C1 in tepkinliği frekans arttıkça azaldığından giriş gerilimi kendisini daha çok R1 üzerinde gösterir, düşük frekanslarda C1 in tepkinliği arttığından giriş gerilimi daha çok C1 üzerinde belirir. Bu bir alçak geçiren filtre oldu, kesim frekansımız f=1/(2*pi*R*C)

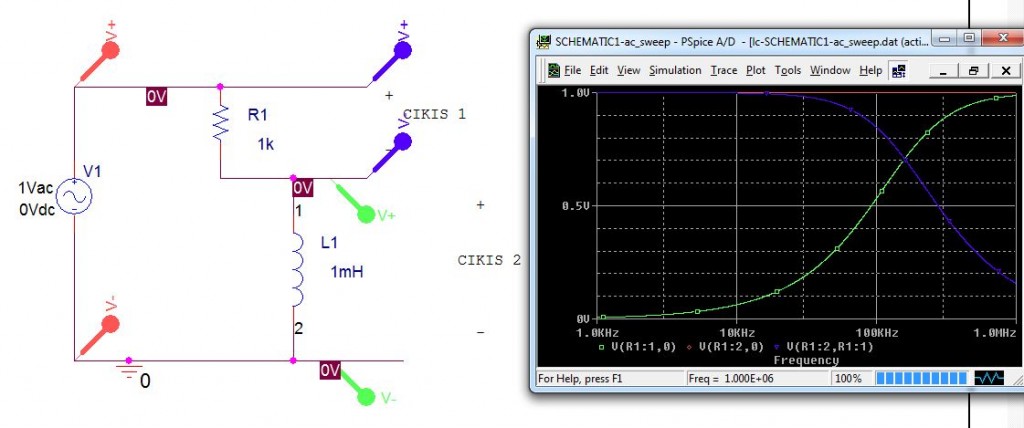
C yerine L koysaydık ki tepkinlik değişimi C nin tam tersiydi, bir yüksek geçiren filtremiz olacaktı:

Bu yazıda çıkış olarak hep çıkış2 yi kast ettik, son örneğimizde çıkış2 yüksek frekansları geçirirken düşük frekansların da çıkış1 de belirdiğini görüyoruz. Önceki devrelerimizi de bu açıdan değerlendirebiliriz, yani alçak geçiren filtre yaptığımızda, düşük frekanslı işaretleri alırken yüksek frekanslıları da diğer kola bıraktığımızdan yüksek geçiren filtre de yapmış oluyoruz. Yukarıdaki devrede çıkış1 alçak geçiren davranış gösterirken çıkış2 yüksek geçiren davranış göstermektedir.

Pratikte filtre kullanımında(düşük frekanslarda <.5 GHz) yukarıdaki mantıklardan pek de farklı durumlar yok. Seri ve paralel rezonans yapılarıyla çeşitli filtreler gerçeklenebilmektedir. Filtre tasarımında kullandığımız elemanların frekans cevabı önemlidir, elemanların L-C değerleri frekansla değişebilir veya belirli bir frekanstan(SelfResonansFrekansı) sonra davranış tamamen(L>C veya C>L gibi davranabilir) değişebilir. Kullanılan kapasitenin türü(seramik, polyester, tantal…) veya induktor ün türü(aircore veya nüveli) dikkatle seçilmeli, mümkünse bir empedans analizör/nw analizör ile elemanlar kontrol edilmelidir .Kullanılan elemanların ESRsi(equivalent/effective serial resistance) veya  Q değerleri de filtrenin cevabını etkiler, düşük Q değerli(veya yüksek ESRli) elemanlar filtrenin keskin cevabını yumuşatır ve filtrenin  dilimize “araya girme kaybı” olarak çevrilen insertion loss unu arttırır. Buraya kadar bahsedilen parametreler SRF, ESR(veya Q) en kolay bir empedans analizörüyle ölçülebilmektedir, eğer bir empedans analizörümüz yoksa fonksiyon jeneratörü-osiloskop ikilisiyle uğraştırıcı da olsa ölçülebilir diye düşünüyorum.

Eleman değerlerinin sıcaklığa göre değişimi özellikle “fine tuned” filtrelerde problem olabilir. NPO(COG) dielektrik malzemeli kapasitelerin sıcaklıktan daha az etkilendiği söylenmektedir. (Bu durumu tecrübe etmek henüz nasip olmadı)

Filtre tasarımında ücretsiz birçok yardımcı program vardır, bunlardan bazıları: AADE Filter Design ve  Windipoles. ODTÜ’de birçok master ve doktora çalışmalarıyla desteklenerek geliştirilen FILPRO programı DOS arayüzlü olsa da kullanışlı ve güçlü bir filtre tasarım programıdır.

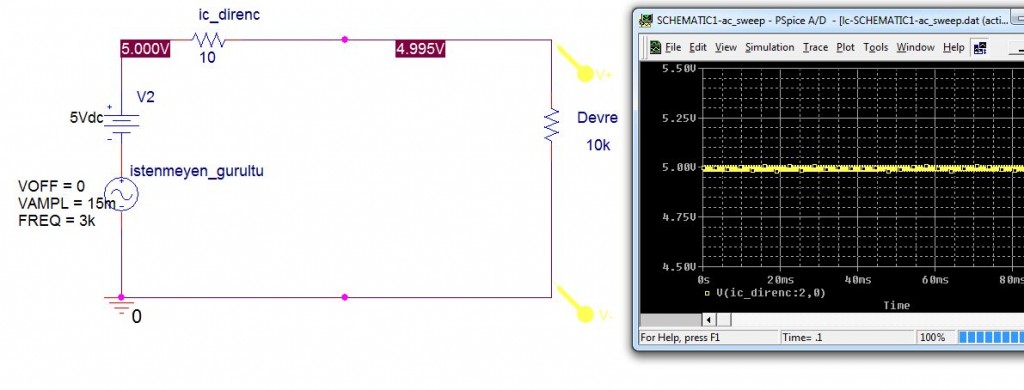
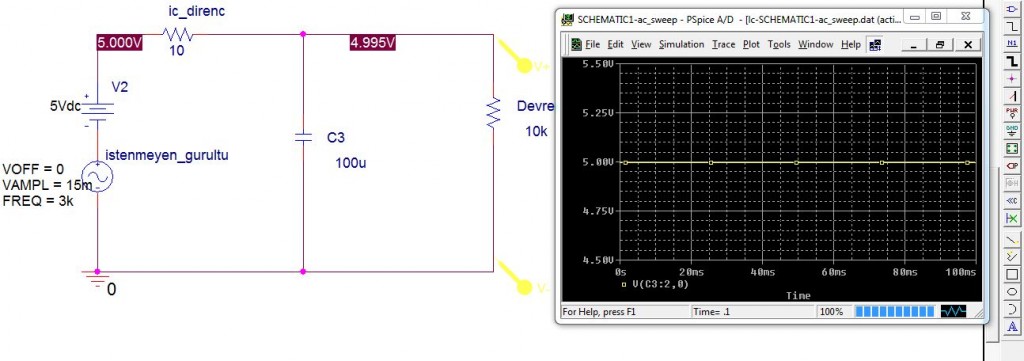
En yaygın olarak paralel veya seri bağlı C elemanları ile birinci mertebeden alçak/yüksek geçiren filtreler kullanıyoruz. Mesela besleme devremizin çıkışına paralel C bağlarız, bu durumda elde ettiğimiz devre ic dirençle beraber düşünüldüğünde yukarıdaki örnek gibi bir alçak geçiren filtre olur:

Yükseltici devrelerimizde girişe ac sinyalimizi uygularken seri bir kapasite bağlarız, o kapasite de yüksek geçiren filtre görevi görür, yüksek geçiren filtre koyarız çünkü ac diye düşündüğümüz işaretin küçük de olsa dc bileşeni varsa kutuplama devresinin dc seviyesini bozar, girişin önüne seri bağlanan bir C girişe baktığımızda göreceğimiz dirençle(Rin) beraber düşünüldüğünde yüksek geçiren filtre görevi görür, o kapasite “dc blocking” kapasite olarak yapılan işlem “ac coupling” olarak da geçer.