Faz Farkı

Mühendislikte Kompleks Sayılar

Son güncelleme: 17 Ocak 2012

Elektronik mühendisliğinde kompleks sayılarla sinyaller ve sistemler dersinde tanışılır, devreler ve sistemler dersiyle tanışıklık gelişir ve sonrasında alınan hemen tüm derslerde kompleks sayılar kullanılır.

Bizler, kompleks sayılara karşı hep bir mesafeli durmuşuzdur, i sayısının ne olduğu sorusu ve kompleks sayıların matematiğe nasıl girdiği sorusu hep cevapsız kaldığından bu mesafeli duruş öğrenim yıllarından meslek hayatına kadar uzar gider… Sonra da geride kaldı denir ve bir kenara bırakılır. Kompleks sayıların temsil ettikleri büyüklükleri pek hissedemeden uzaktan uzaktağa hesap yapar, doğru sonuçlar da buluruz ama bu hesaplar  hep tatsız hesaplardır çünkü tam anlayamadığımız ve içimize sindiremediğimiz bir cebir kullanmışızdır, kompleks cebir. 

Kompleks cebir ve biraz daha ötesi “complex calculus”. Kompleks cebirde; sadece toplama, çarpma işlemleri tanımlıdır. Complex calculus’da  kompleks düzlemde türev ve integral işlemleri de dahil olmaktadır.

Lisanstan sonra “kompleks değişkenli fonksiyonlar teorisi” dersini alıp biraz da bu ders üzerine yoğunlaşınca kompleks sayıların iki boyutlu bir sayıdan ibaret olduğunu ve kompleks cebrin kendi içerisinde cebrik kuralları olan basit bir sistem olduğunu düşünmeye başladım. Kompleks sayıları benimsemenin ve elektronikte gönül rahatlığıyla kullanmanın kok(-1) in manasının tırtıklanmasıyla hiç alakasının olmadığını gördüm.

Kompleks değişkenli fonksiyonlar kullanageldiğimiz reel fonksiyonlardan daha genel ve daha fazla içerik taşıyan fonksiyonlardır. Kompleks değişkenli bir fonksiyon; sayı doğrusundan seçme bir değerin fonksiyonu değil bir düzlemden seçme iki boyutlu bir sayının fonksiyonu olduğu gibi bu fonksiyonların sonucunda ürettiği sayılar düzlemde bir noktaya karşı düşen iki boyutlu sayılardır. Mesela f(z)=z^2 fonksiyonu kompleks düzlemde hangi değerleri nerelere atar… tek başına incelenesi bir olay. Bu fonksiyonun reel fonksiyonlardaki gölgesi f(x)=x^2 basit bir eğriyle gösterilebilecek yavan bir fonksiyon.

exp(i*z) fonksiyonu mesela, kompleks değişkenli bir fonksiyon, farklı z değerleri için hangi değerleri üretir acaba? z=1+4i için? z=2+5i için nasıl değerler üretir… z=1, 2, 3, 4, 5, 6… gibi reel değerler için kompleks düzlemde bir çember çizdiğini biliyoruz.

Meşhur Euler eşitliği vardır: exp(i*z)=cos(z)+i*sin(z) bu eşitliğin farklı yollardan ispatı olduğu gibi en kolayı exp(i*z) nin taylor seri açılımının cos(z) nin açılımı + i* sin(z) nin açılımı olduğunun gösterilmesiyle yapılan ispatıdır.

exp(i*t) fonksiyonu kompleks değerler üreten bir fonksiyondur, reel kısmı cos(t) üretirken sanal kısım sin(t) üretir. İki kompleks fonksiyonun toplamıyla saf reel bir fonksiyon elde edilebilir: exp(i*t)+exp(-i*t).

AC analizde karşımızda çıkan karmaşık sayılar ya bir sinüzoidal temsil eder(özel adı:fazör) ya da bu sinüzoidaller arasındaki ilişkiyi ifade eder(özel adı:empedans). Kompleks bir oran reel bir orana göre daha zengindir, hem genlik hem faz değişimi söyler çünkü. Mesela AC kaynaklı bir devrede bir kapasite elemanının akımı ile gerilimi arasındaki ilişki türevli tanım bağıntısı yerine genlik oranı ve faz farkı söylenerek tanımlanabilir. Genlik oranı ve faz farkı da kompleks cebirde çarpma işlemiyle ifade edilebilmektedir. Örneğin x işaretinin başına gelen “genlik yarıya düştü faz 30 derece geri düştü” işleminin tam karşılığı x*0.5*exp(-i*pi/6) işlemiyle ifade edilebilmektedir.

LTI(linear time invariant-doğrusal zamanla değişmeyen)  sistemler girişlerine gelen sinüzoidalin frekansını değiştirmezler,  girişe gelen sinüzoidalimiz çıkışta sadece genliği ve fazı değişmiş olarak belirir. Örneğin aşağıdaki 1kHz lik işaretlerden mavi olan girişe gelen sinüzoidal, kırmızı olan çıkışta beliren olsun.

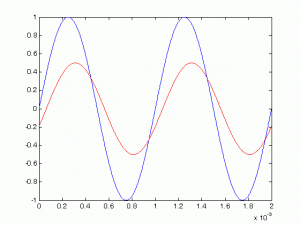
Görüyoruz form aynı ancak faz ve genlik farkı var! Şimdi siz bu sistemin girişteki sinüzoidal üzerindeki etkisini nasıl ifade edeceksiniz? İşareti yarıya düşürür desek, y=0.5*x deriz ama faz da değişiriyor!
Sadece fazı pi/8 kaydırır desek o da olmuyor. Sonuçta genlik de değişiyor. İşte kompleks cebirdeki çarpma işlemi bir sayının hem büyüklüğünü hem de açısını değiştirebiliyor. Ben buna modifiye etmek diyorum. Kompleks çarpım  çarptığı sayının genliğini ve fazını değiştirir, sayıyı modifiye eder. Bu yüzden transfer fonksiyonlarımız farklı frekanslarda farklı “modifiye eden sayılar” üretir. Örn:

H(w)=1/(1+i*w*0.001) transfer fonksiyonu f=1kHz de 0.0247 – 0.1552i sayısını yani  0.1572, aci=-0.45*pi üretiyor. Bu da demek oluyor ki bu sistem 1kHz de gelen bir sinüzoidalin genliğini 0.1572 ile çarpar fazını da 0.45*pi kaydırır.